For some students, math is complicated enough. Even when it consisted of counting on fingers and grouping blocks in an effort to grasp the concept of multiplication, it sometimes still proved challenging. In 2009, the National Governors Association Center for Best Practices (NGA Center) and the Council of Chief State School Officers (CCSSO) announced that 49 states and territories, including Missouri, would adopt Common Core standards for certain subjects.
In mathematics, these standards aim to increase students’ problem-solving abilities, help them use reasoning and contextualization to solve problems and utilize the structures of equations to come up with solutions, according to corestandards.org. While these sound like reasonable goals, many parents of elementary school students detest Common Core standards, saying they are too difficult for them–let alone their children–to figure out.
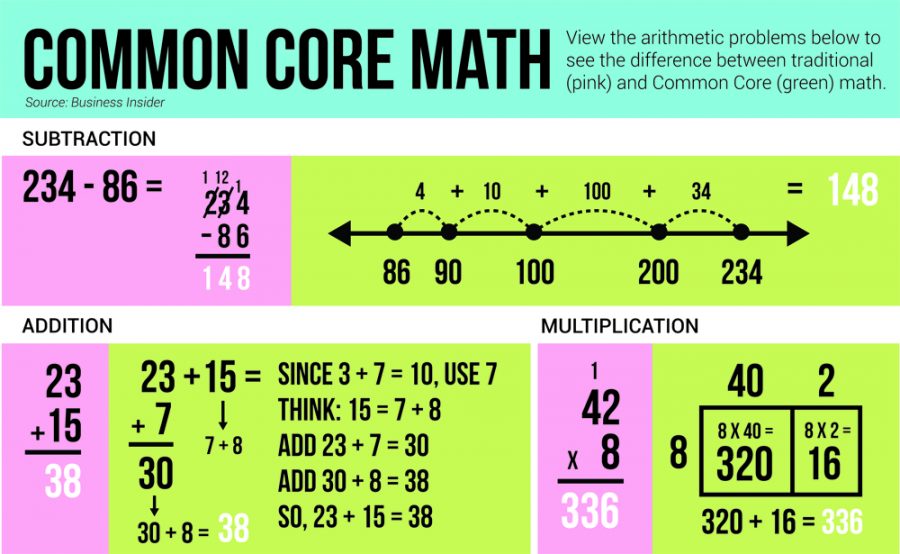
At first, these allegations seem understandable. In an addition problem such as 23+15, “traditional” arithmetic would require students to simply stack the numbers on top of each other and add the numbers in their respective columns to get 38; however Common Core standards teach to first add a number to the three in 23 to get 10. That factor is seven, so the next step is to see what adds to seven to get the 15 in the original expression. Seven and eight make 15. The fourth step involves adding 23 to seven to get 30, and then finally adding eight to 30 to get 38. After figuring those steps out, one can use that outcome to say that 23+15=38.
While this may seem like a pointless way of complicating an otherwise easy problem, many mathematical experts such as Dr. William McCallum, a professor at the University of Arizona and author Arizona’s K-12 math standards, believes it is important for students to be able to not just do math but be able to explain it and understand that the entire number system is based on the number 10. With Common Core standards, teens in higher difficulty math classes will be able to recognize how certain problems are similar to ones they completed in elementary school.
“The most important thing about the Common Core from my point of view is that it represents an agreement between states about the mathematical ideas and skills that students should learn in each grade level. But it does not propose any grand new scheme about how they should learn those things,” Dr. McCallum said. “There is nothing new about the ideas and skills in the Common Core; mathematics is still the same as it always was. Different people have different ideas about how students should learn, and sometimes people have identified those ideas as coming from the Common Core.”
RBHS math teachers try to instill more than a basic understanding of concepts in students by discussing how  methods for how to help students understand concepts and apply mathematics to practical issues, College Algebra and AP Calculus BC teacher Burke McCray said. He agrees with McCallum that students who begin using Common Core techniques at an earlier age become better at problem-solving.
“One of the tenets of Common Core is that students have a conceptual understanding of the topics in each class. As students progress in mathematics, the concepts become become more abstract. It’s harder to succeed with those abstract concepts if the students are just memorizing algorithms,” McCray said. “Common Core isn’t about giving one method for students to use but, instead, helping students understand more deeply and giving them more than one way to do things. Students learn differently. The more options they have, the more likely they will find at least one that will work for them. I think that’s a good thing.”
Sophomore Leo Zhuang also believes Common Core math is beneficial and helps people eventually understand more complex problems. Zhuang, who took Calculus III and Differential Equations at the University of Missouri-Columbia (MU) last year and will take AP Statistics next year, said he used Common Core standards from elementary school up until Algebra 1.
He said Common Core math is the same as traditional math but takes more time, and many of the “extra” concepts taught in common core math are often used in mental math.
“Many think that common core math is stupid, redundant and takes too long. In the end, however, you learn the same concepts of math. I think schools that don’t teach common core should attempt to incorporate it. The thing with common core math versus traditional math is that traditional math cuts corners. Having learned through the traditional way, it doesn’t always address the underlying reasoning behind processes,” Zhuang said. “In Common Core, the process is elaborated and often slow. For example, you can just memorize a multiplication table or go through the long process of working out problems such as doing five times three by doing 5+5+5.”